こんにちは、ウチダです。 今日は、小学6年生および中学1年生で習う 「比例・反比例」 の式のグラフの書き方や比例定数の求め方、またそれらの意味や代表例についてわかりやすく解説していきます。 ※この記事では比例と反比例をセットで解説していきま反比例の式から、グラフを書きましょう。比例や反比例の式をグラフにするのは、案外簡単です。反比例の式にxの値を入れて、その値から求まるyの値をプロットし、線をつなぐだけです。 例えば、 y=1/x 下図のグラフが書けました。これが反比例のグラフ反比例のグラフは双曲線! 反比例のグラフ書き方の手順 表を書く グラフに点を取っていく 点をなめらかに結んだら完成! 反比例のグラフ書き方 まとめ! がんばっているのに60点の壁をクリアできない中3生の方へ こちらの関連記事はいかがでしょう

比例のグラフ 無料で使える中学学習プリント
比例 反比例 グラフ 読み取り
比例 反比例 グラフ 読み取り-比例とは? 簡単にいうと、比例とは・・・ 比例=比が等しい y=ax(aは0でない定数) グラフは原点を通る直線 ちょっとわかりやすく説明するわね。 比例というのは、片方が2倍・3倍となる時、もう片方も2倍・3倍と同じようになること。 つまり、 比数学14章比例・反比例「反比例の表,式,グラフ」<準備問題> 組 番 名前 1次の(1)~(3)について,yをχの式で表しなさい。また,このうちyがχに反 比例するものを選びなさい。 (1)面積が12㎝2の長方形の縦の長さをχ㎝,横の長さy㎝。



グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
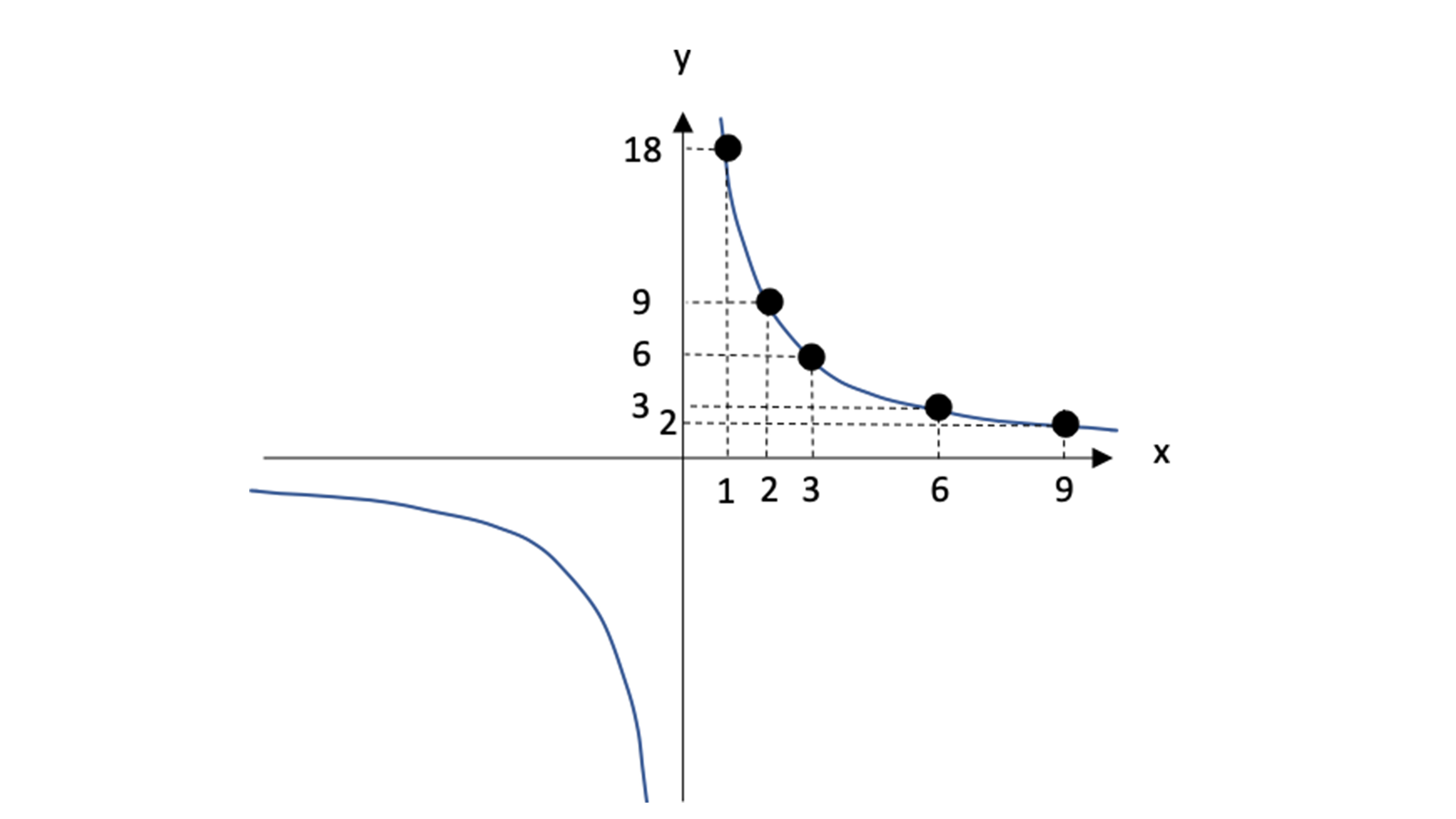
比例・反比例のグラフ 《問題》 次の式に対応するグラフを,右から選びなさい. (ルール:式を一つクリックし,続けて「 対応するグラフ 」をクリックすると消えます.全部消えたらできあがりで反比例のグラフはわかりにくいですが、xの値の変化量とyの値の変化量を掛け合わせた時に常に一定の比例定数aで推移する関係のことを反比例といいます。 上のグラフの場合は、 x=1の時y=8なので、1×5=8 x=2の時y=4なので、2×4=8 x=8の時y=1なので、8×1=8 とこのページは、 中学1年生で習う「反比例のグラフの問題集」が無料でダウンロードできる ページです。 この問題のポイント ・2つの変数xとyが反比例の関係の時、式の形は下のようになります。 y = a x ・比例定数:aが正の数や、負の数のときのグラフを
─ ─ ─ 21 ─ 4 右の図は反比例のグラフで,グラフ上の点Pの座標は(6,9)である。 これに ついて,次の問いに答えなさい。 ⑴ このグラフ上の点で,x 座標,y 座標がともに整数となる点は何個ありますか。 ⑵ このグラフ上で,y 座標が 18 の点を S ,2 の点を T とする。次はグラフから式を求める方法を確認しましょう。 これは、反比例の定数 $\textcolor{blue}{a=xy}$ を使えばすごく簡単です。 例題次の(1)~(3)のグラフの式を求めなさい。 STEP $\textcolor{blue}{1}$ :曲線上に点を $\textcolor{blue}{1}$ つとり、座標を求める反比例のグラフ 基本比例のグラフ で見たときと同じようにして、反比例のグラフをかいていきます。 x と y の値の対応表を書いて、対応する点をとっていく、という流れです。 y = 6 x のグラフを考えてみます。 x が 1 から 6 までの整数の値をとると
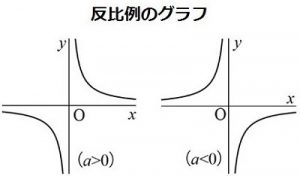
3 回答 負の比例と反比例の違いは何ですか? ? テキストグラフでこの二者が書かれています。 負の比例は右下がりの直線(\)で描かれています。 反比例は、右下がりの直線(\)を原点に対して凸で描かれています。 でも、混同して反比例のグラフ 反比例のグラフは双曲線と呼ばれています。 例えば、 a = 2 のグラフを見てみましょう。 表の x と y の座標位置に点を打って繋げるとグラフになります。 図のように、1つの式で2つの曲線ができるので、 双曲線 と呼ばれているのです。 ポイント! 反比例では x = 0 には絶対になりません。 0 で割ってはいけない数学のルールに反するからです。 また、 y = 0 にもなり比例のグラフ書き方 まとめ 比例のグラフを書くためには以下の手順通りやればOK! 原点に点をとる 比例定数を見て、分母の数だけ右へ分子の数だけ上下に動かしたところに点をとる 2点を線で結ぶ 手順②は、慣れるまで少し難しく感じるかもしれませ




反比例の表やグラフの性質 問題の解き方 小学生に教えるための解説 数学fun



Wordで使える 中学数学のグラフ用紙 Wordで数学問題プリントを作ろう
代入するxの値を工夫しよう! y=axの形のグラフは、通る1点を調べて原点と結べばいいんだね。 ただし、今回のように比例定数が分数になっていると、少し注意することがあるよ。 試しに、x=1 を代入してみよう。 x=1のとき、y=2/3 だね。 でも、(1それでは、実際にグラフを書いてみましょう。 グラフが通る点を取っていくために、まずは反比例の式に を代入します。 を に代入すると このことから、反比例のグラフは のとき を通るということが分かります。 かず先生 これで点が1つ取れたね! あとは 、 と同じように点を取っていけばOKだよ を に代入すると を に代入すると を に代入すると を に代入すると を に代入すると こう反比例のグラフで気を付けたいところ 反比例のグラフではもう1点気を付けたいところがあります。 それはグラフの先の方です。 下のグラフに入れた赤丸の部分です。 右側の赤丸の部分は、右に行けば行くほど\(x\)軸に段々近づいていきます。




比例のグラフ 無料で使える中学学習プリント




中1数学 比例のグラフ1 Y 2xなど 映像授業のtry It トライイット
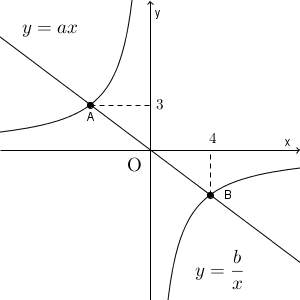
2つの反比例のグラフ おわりに 比例と反比例のグラフ 例題1 次の図は、 y = a x と y = b x のグラフです。点A, Bはこれらのグラフの交点です。 点A の y 座標は 3 で、点B の x 座標は 4 です。 このとき、 a, b の値を求めなさい。 比例定数がわかっていませんが、これを求めるには、 標準比例のグラフ や 標準反比例のグラフ で見たように、通る点の座標がわかっていればいいでエクセルで反比例のグラフを描く方法 求められた計算結果をもとに、反比例のグラフを作成していきましょう。 xとy両方の数値範囲を選択し、上タブの挿入、散布図、平滑線と選んでいきます。 すると、以下のような反比例のグラフができました。 後はX 』ですが、算数・数学において 「数字を0 0 で割ってはいけない」 というのは常に付きまとうルールだからです。 これ理由については以前ま



比例 反比例のグラフと図形 中学1年数学 Youtube
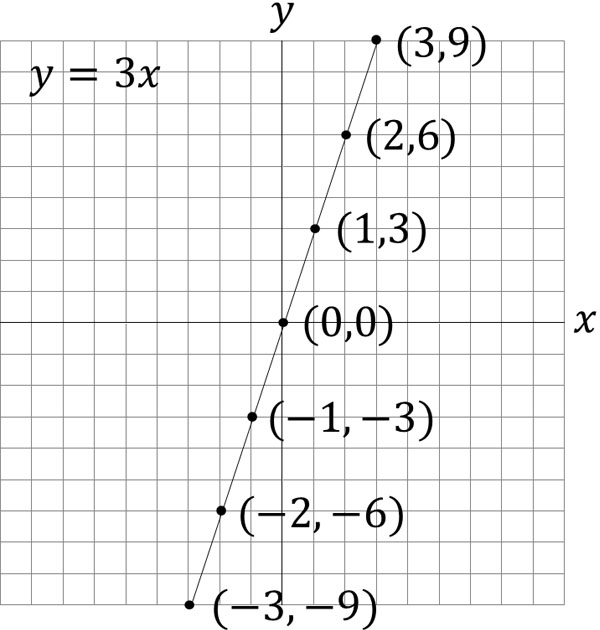



比例と反比例 中学数学の座標の読み方とグラフの式の求め方 Hatsudy 総合学習サイト
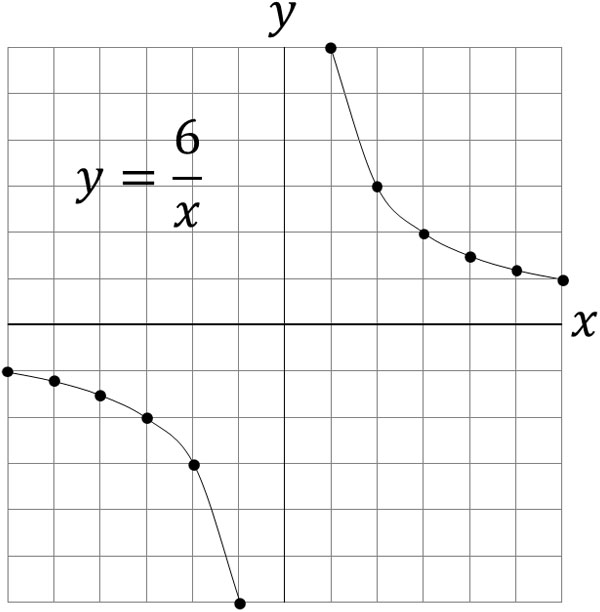
中1数学。「反比例のグラフ」をかけ。「y = 6/x」ハァァ? x 軸にも y 軸にもくっつかない理解不能(ガクッ)おや、中学生が倒れそう。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 反比例など一発! コツを語る無料サイト。比例のグラフ 小学校で扱うグラフは正の範囲のみでしたが、中学校数学からは負の範囲まで拡張します。 ただし比例の2つの性質は変わりません。 比例のグラフの特徴 原点を通る 直線 下の図は y=2x y = 2 x と y= −2x y = − 2 x のグラフを表しています。 比例定数が負になると x x が増えるごとに y y は減っていくので右肩下がりのグラフになるのです。 また、 x x や y y などの変数の取りうる範2 y は xに反比例し ,=4 のとき y 12 である。のとき 次のいに答えよ。 ⑴ y をx の式で表せ。 ⑵ x=3,x=-8 のときのy の値をそれれ求めよ。 3 次のの ,は比例のグラフ ③ は反比例のグラフである。 y をx の式で表せ。 4 次のいに答えよ。 ⑴ y=- 4 3 x の



Studydoctor比例のグラフの利用 動点の問題の解き方 中学1年数学 Studydoctor




反比例とは何かが例で即わかる 公式 グラフの書き方も即理解 高校生向け受験応援メディア 受験のミカタ
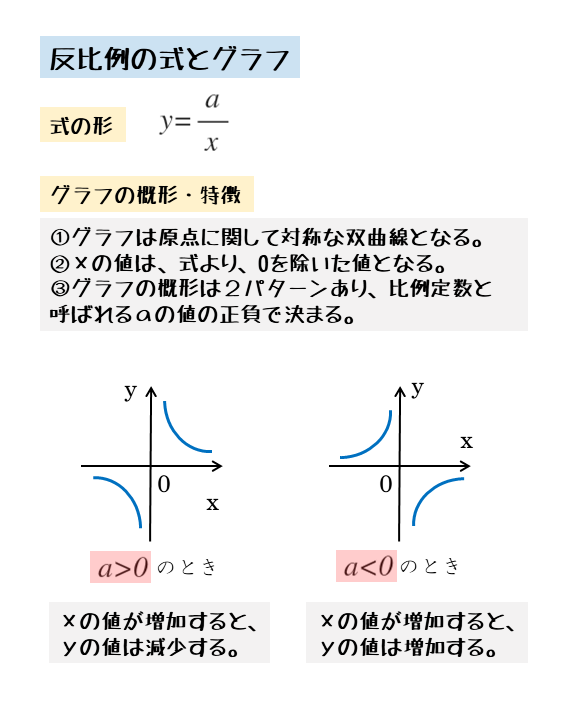
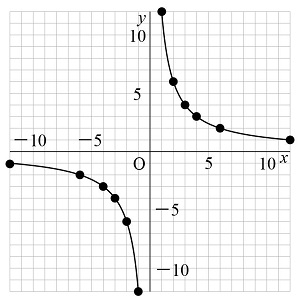
反比例のグラフの特徴 なめらかな曲線になる グラフの重要な性質として、 「x x 方向、y y 方向、どちらにどれだけ拡張してもx=0 x = 0 やy=0 y = 0 の線と交わることはない」 というのを抑えておきましょう。 反比例の式は『 y= y = 決まった数 ÷x ÷反比例のグラフ 反比例の式 を、座標に描いてみよう。 のとき、 になる。 点 を打つ。 のとき、 になる。 点 を打つ。 のとき、右辺の分母が になるので、考えない。 点に沿って、線を引くと、曲線のグラフができあがる。 さらに のとき、 になる。 点 を打つ。 のとき、 になる。 点 を打つ。 点に沿って、線を引くと、反対側にも曲線のグラフができあがる。 のグラフは、離れた曲線が2つあるので、練習 反比例の式とグラフ 反比例の式とグラフ 基本の確かめ 基本的な学習内容に習熟し、それを活 用する。 yがxに反比例するとき、xの値とそれ に対応するyの値の積は、いつも決 まった数になることを理解し、その関 係を式に表す。



1
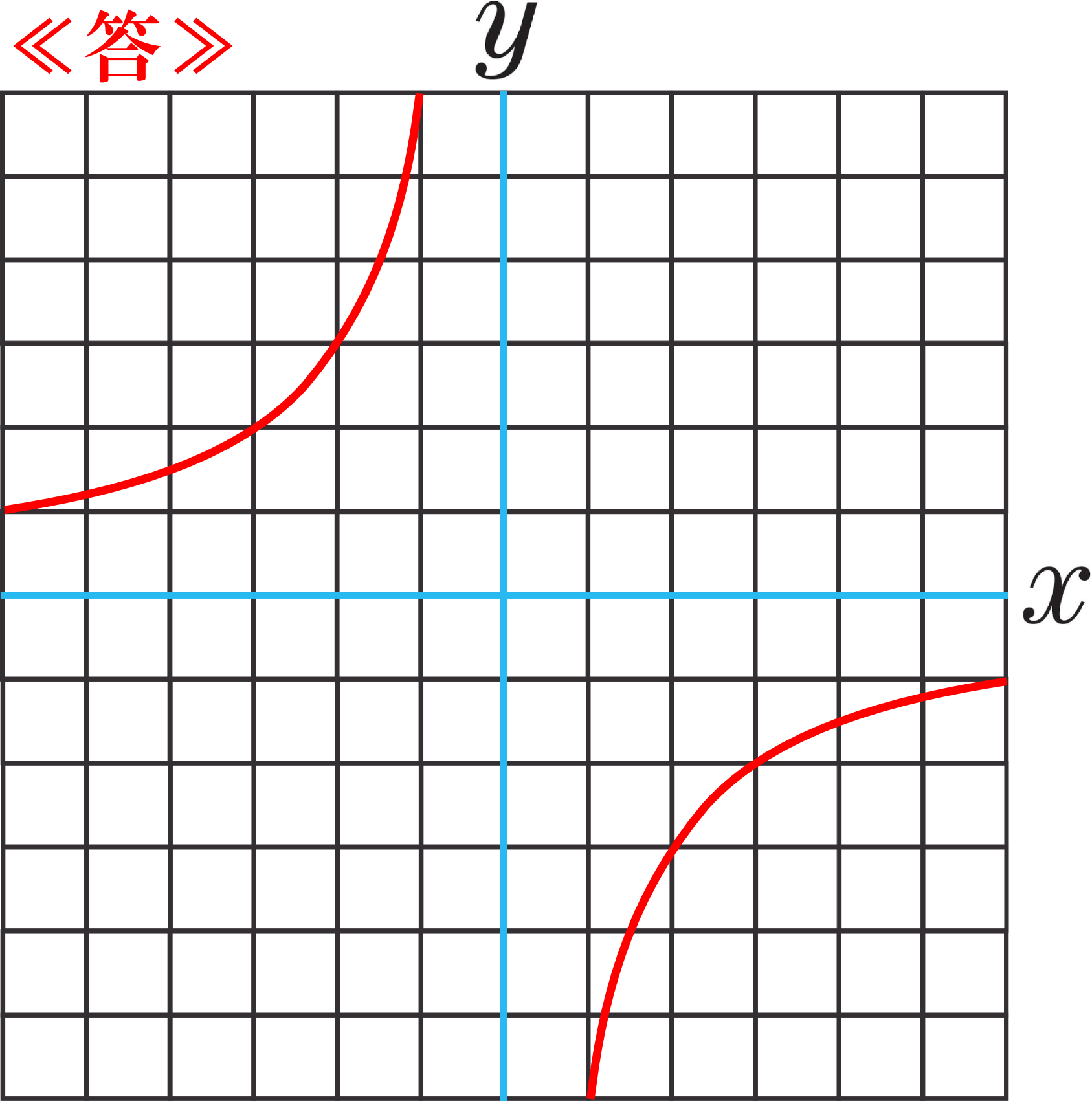



中学1年数学練習問題 比例 反比例 反比例のグラフと関数の解答
グラフ上の平行四辺形 座標平面上の平行四辺形に関する問題と、比例・反比例の総合問題 (応用)について学習します。 平行四辺形 グラフ上の平行四辺形 グラフ上の平行四辺形 グラフ上の平行四辺形 グラフ上の平行四辺形 グラフ上の平行四辺形



グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



比例関係とは 1分でわかる意味 グラフ 正比例との違い 負比例
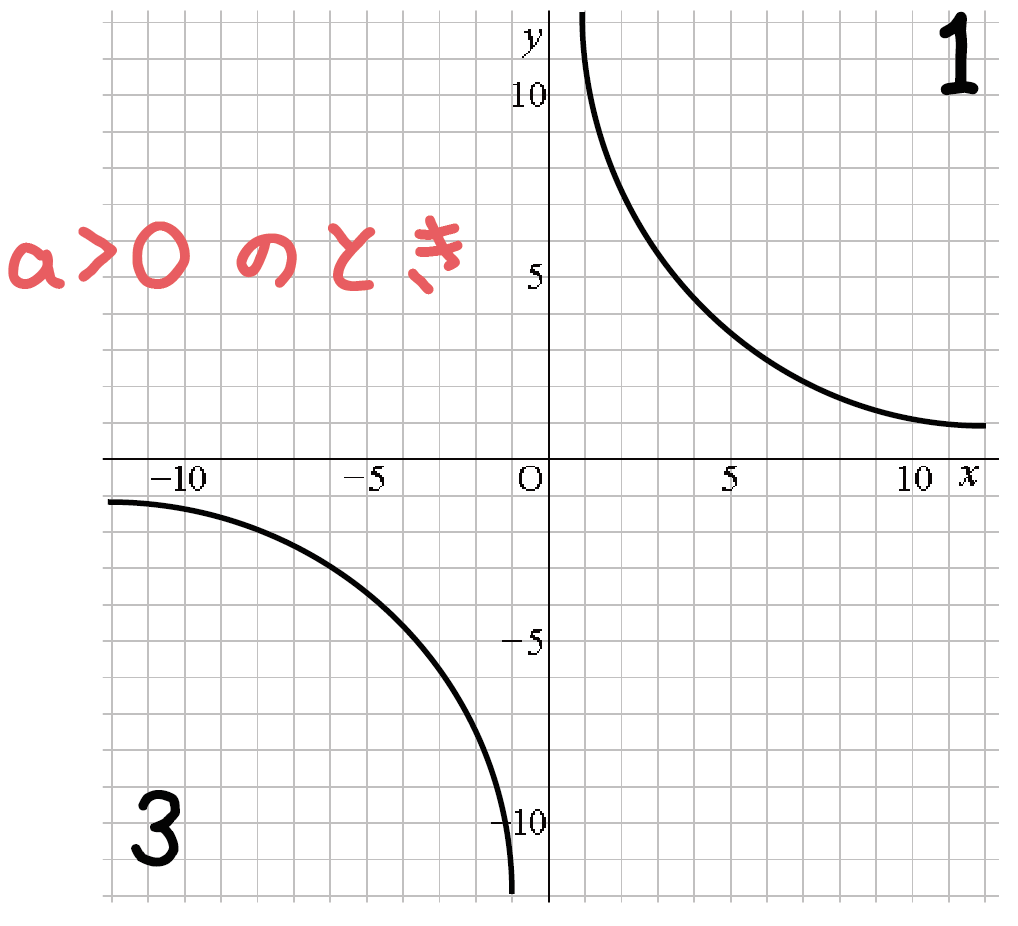



中1数学 反比例のグラフにみられる3つの特徴 Qikeru 学びを楽しくわかりやすく
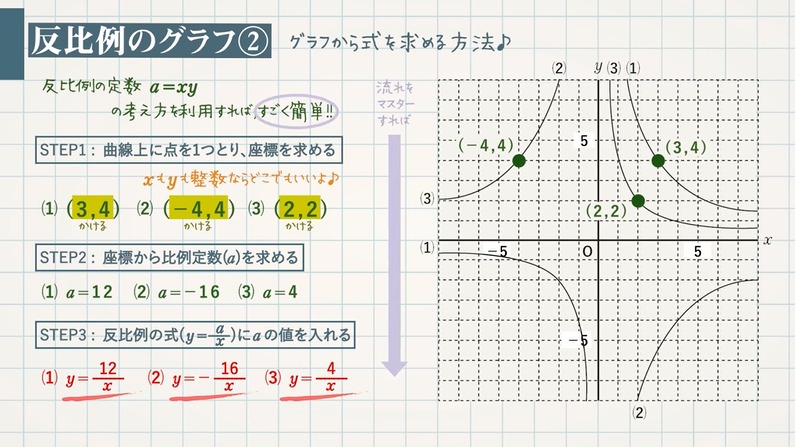



反比例の表とグラフ 教遊者



いざ いざ 実践 比例と反比例 小学6年 算数の教え方教えますmother S Math Happy Study Support




比例と反比例の違いは 見分け方はどうすれば良いか解説 数スタ



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院



反比例のグラフ 比例定数とグラフの形 デジタル教科書 電子教科書




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく




比例反比例の利用ー動点 速さ グラフなどの問題 無料で使える中学学習プリント



Afsoft Website Afsoft Jp



応用 比例と反比例のグラフ なかけんの数学ノート



中学数学 比例と反比例 の教え方 比例の式を求める




反比例のグラフ 無料で使える中学学習プリント




第8回 すなおな反比例 後編 数学ガールの秘密ノート 結城浩 Cakes ケイクス




反比例のグラフ 読み取り 式の作り方と書き方を解説 中学生 中学数学 理科の学習まとめサイト



比例と反比例 1 式とグラフ ファクトリウム
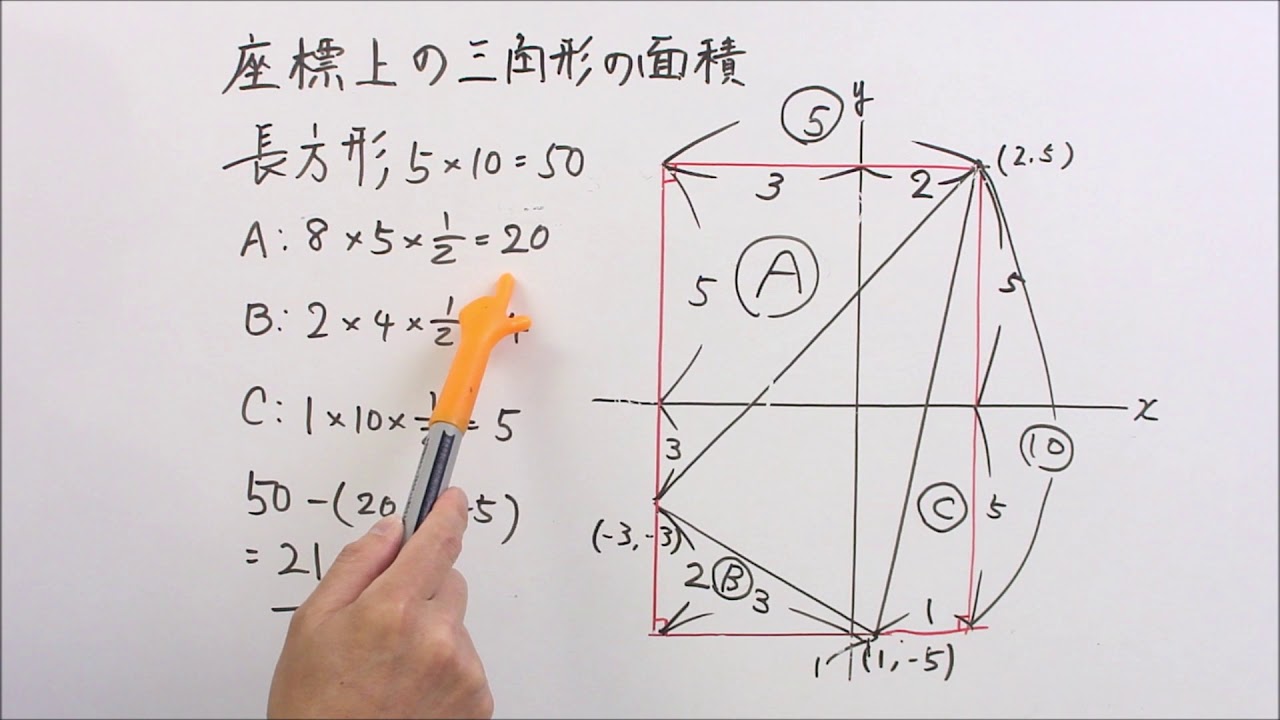



中1数学 比例と反比例 12 2 グラフと三角形の面積 解説 練習問題 Youtube



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典
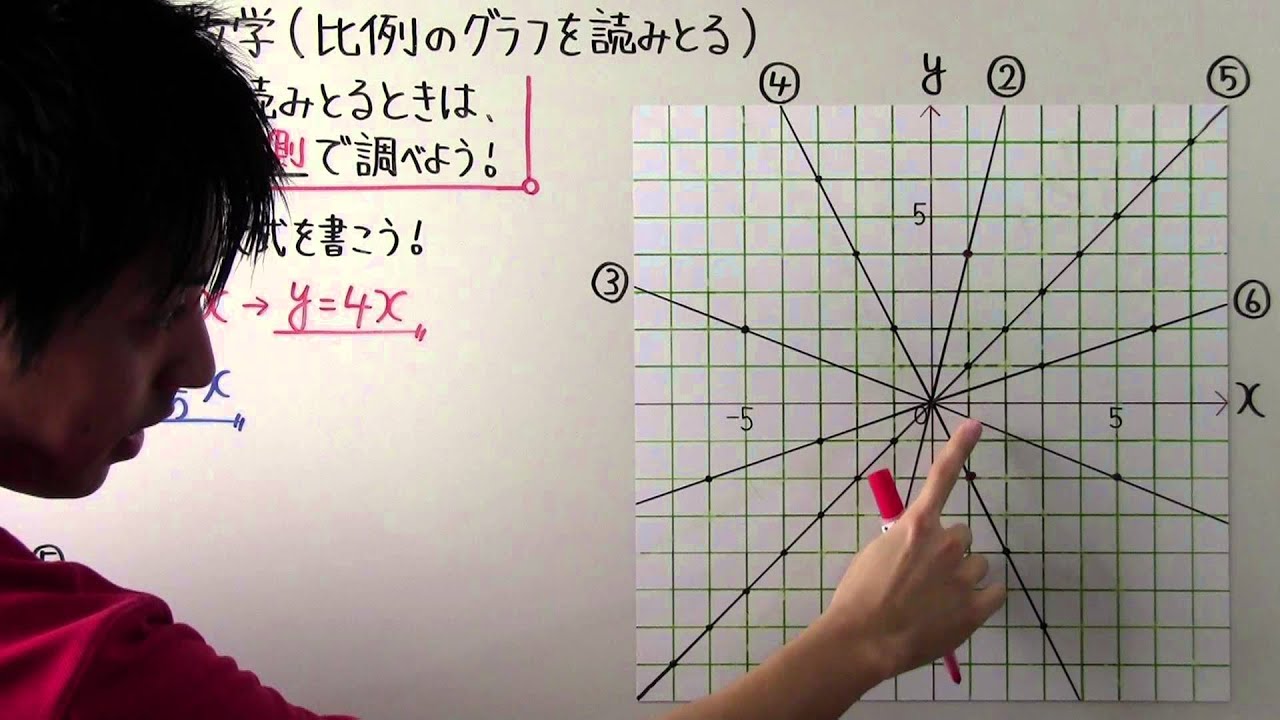



中1 数学 中1 50 比例のグラフを読みとる Youtube




比例と反比例 6 反比例のグラフ 伊東市の家庭教師



なぜ比例のグラフは直線で 反比例のグラフになると曲線なんでしょう Yahoo 知恵袋



中1数学 発展 応用問題プリント 比例と反比例の座標とグラフ 130



中学の比例と反比例の問題です わからないので教えていただけると幸いです Yahoo 知恵袋




スタディピア 関数とグラフ



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典




グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




中学1年生 数学 比例 反比例 問題編 柳 よしひこ Note
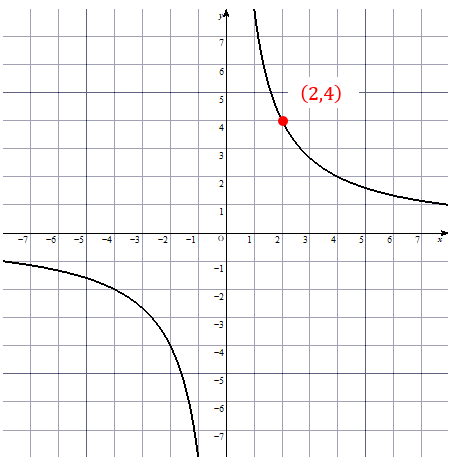



比例 反比例の式 式の作り方 違いは 問題を使って解説するぞ 数スタ




反比例の式のグラフとは 比例定数の求め方 意味や例について解説 遊ぶ数学



中1 比例のグラフ



無料 中1数学 テスト対策問題 解答プリント 121 比例と反比例2 比例2グラフ




比例と反比例はこれで完璧 グラフと式の読み解き方




中学1年生 数学 比例と反比例 反比例 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
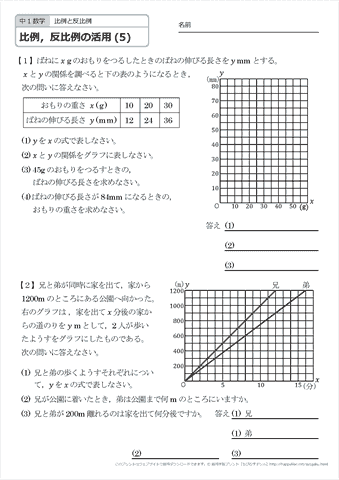



中学1年生 数学 比例 反比例の活用 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



2次関数 関数について 日々是鍛錬 ひびこれたんれん
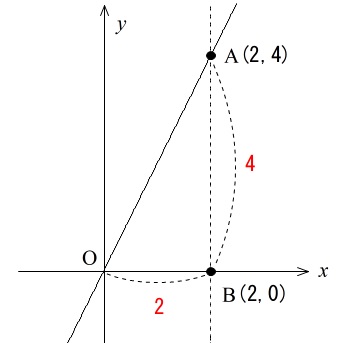



比例と反比例のグラフから三角形 四角形の面積を求める問題の解き方



Studydoctor反比例のグラフと式の求め方 中学1年数学 Studydoctor



無料 中1数学 基本問題 解答プリント 比例と反比例5 反比例のグラフ 132



中1 数学 中1 50 反比例のグラフを書く Youtube




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく




Ma1hirei 2 07 1 Png
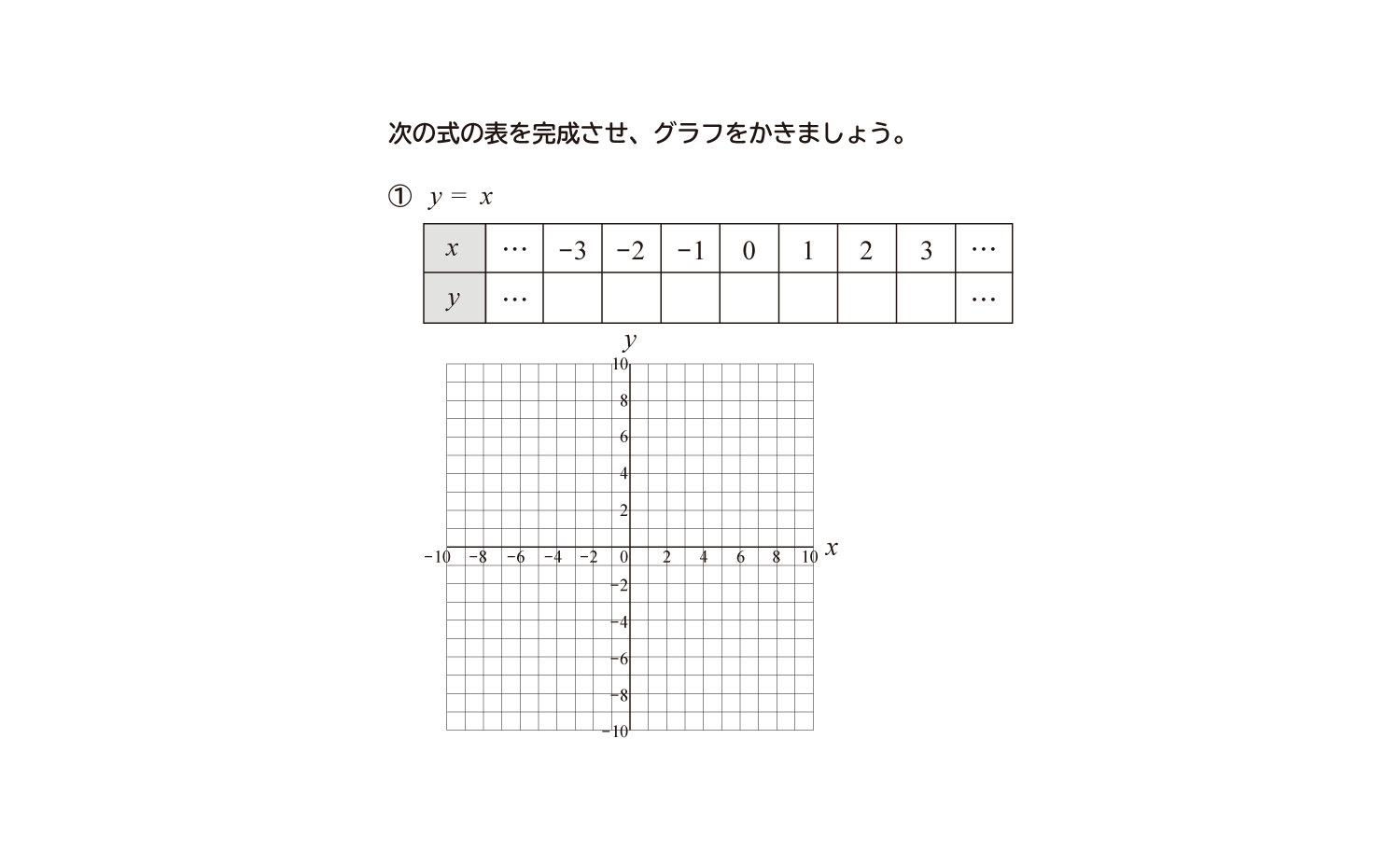



中学1年生 数学 無料問題集 比例のグラフ 比例定数が正の場合 おかわりドリル
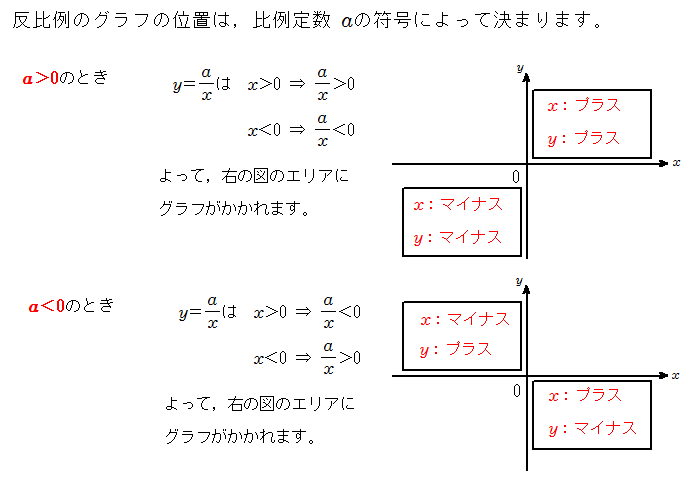



比例と反比例 反比例グラフの双曲線の位置 中学数学 定期テスト対策サイト
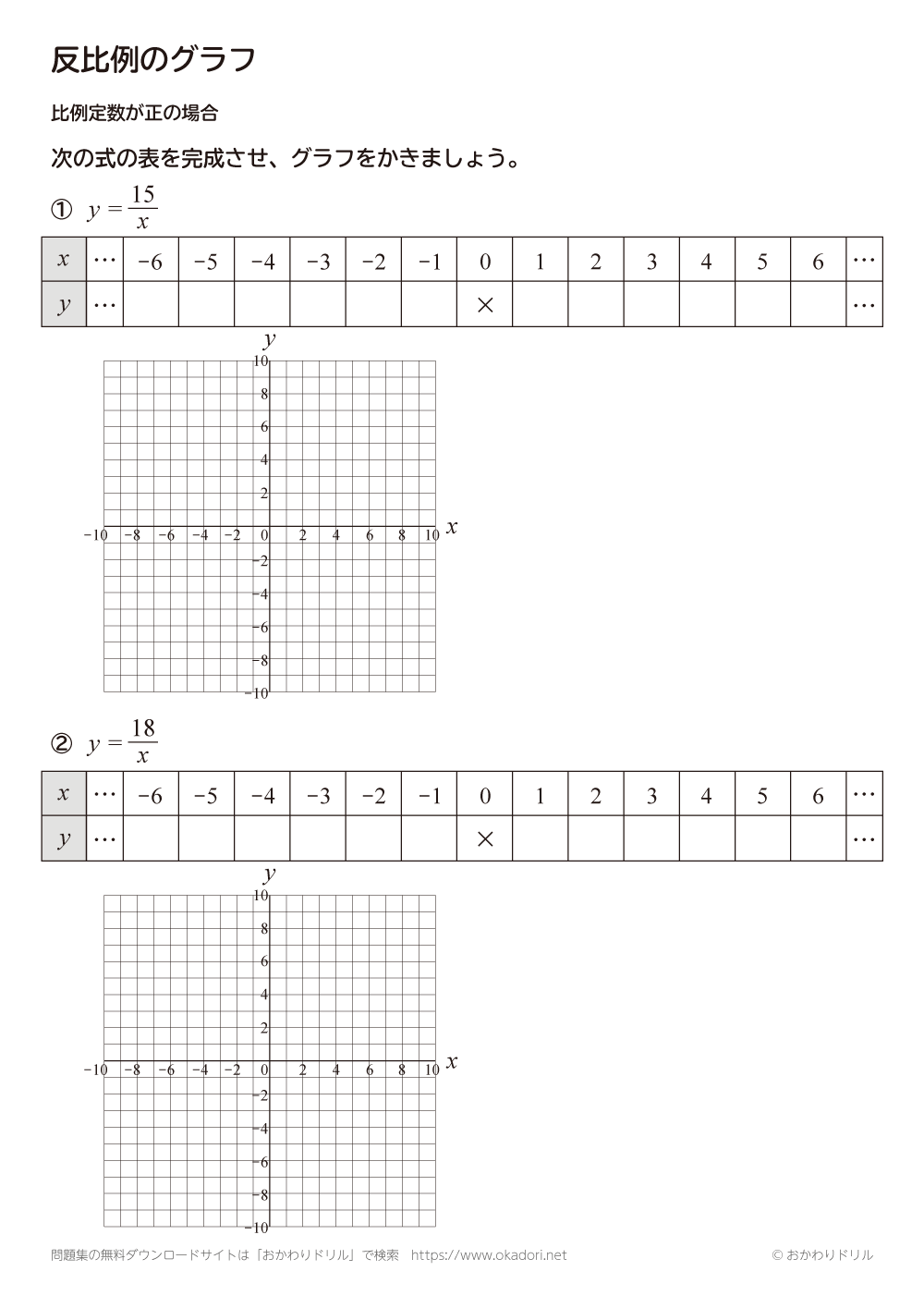



中学1年生 数学 無料問題集 反比例のグラフ 比例定数が正の場合 おかわりドリル
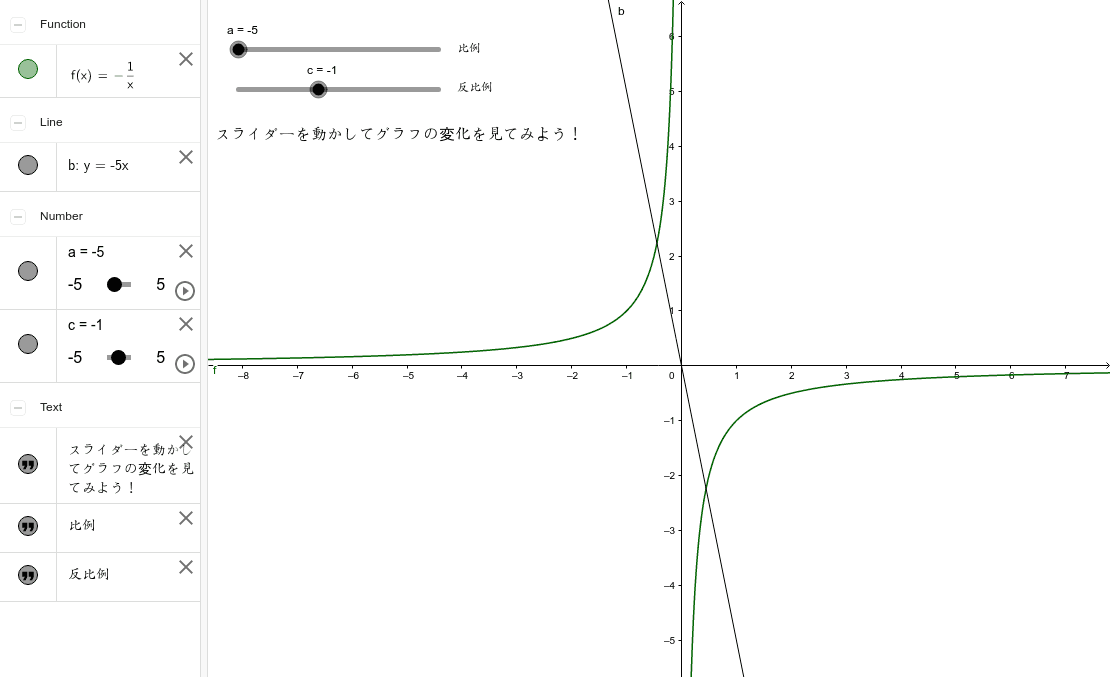



比例と反比例のグラフ Geogebra
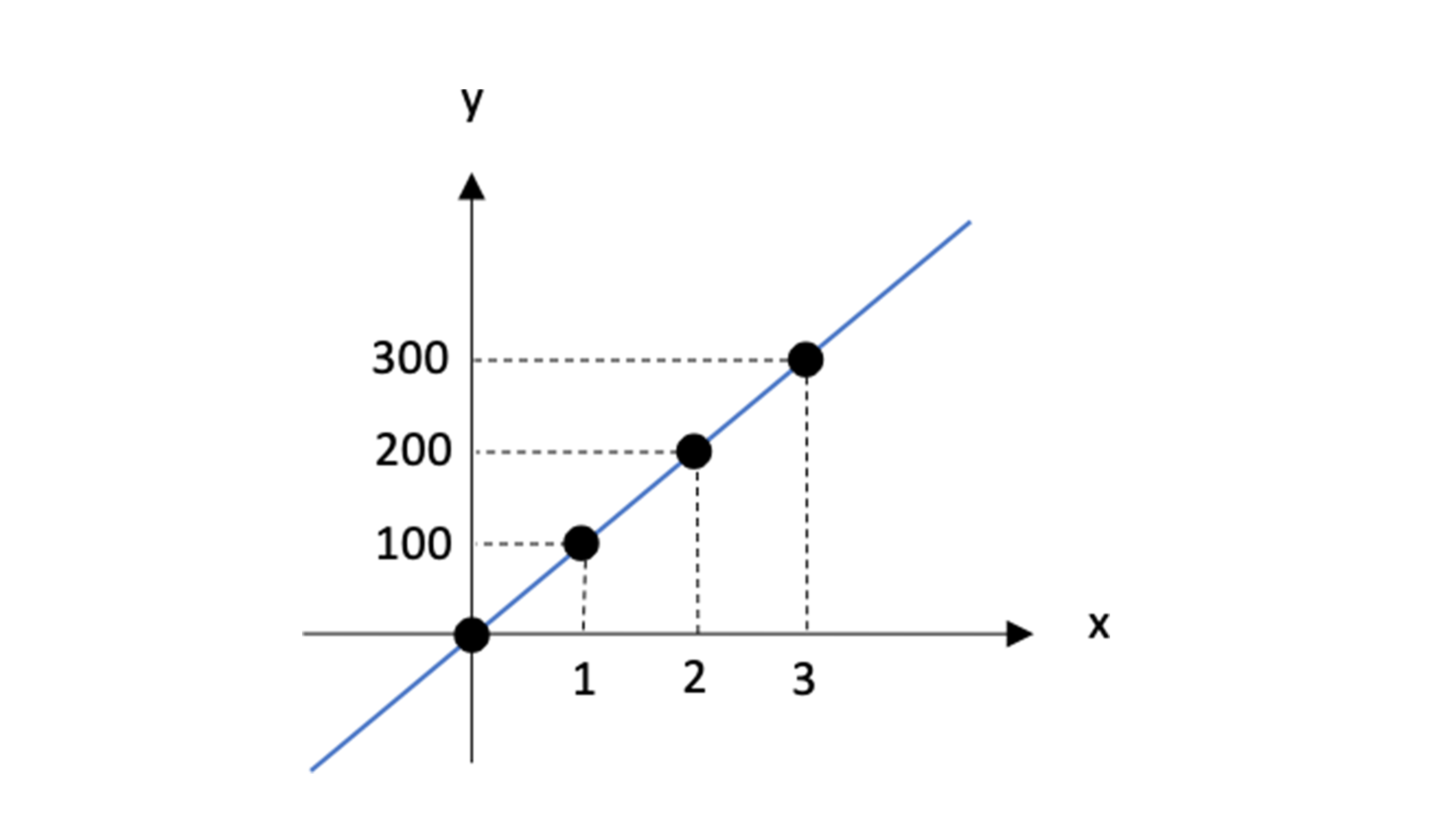



グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院




比例と反比例はこれで完璧 グラフと式の読み解き方



無料 中1数学 テスト対策問題 問題プリント 123 比例と反比例4 反比例2グラフ



Studydoctor反比例のグラフと整数点の個数 中学1年数学 Studydoctor




中1数学 反比例のグラフ 練習編 映像授業のtry It トライイット




グラフの特徴 書き方 読み方をマスターしよう 比例と反比例 中級編 中学受験ナビ



Studydoctor反比例のグラフの形と書き方 中学1年数学 Studydoctor



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院
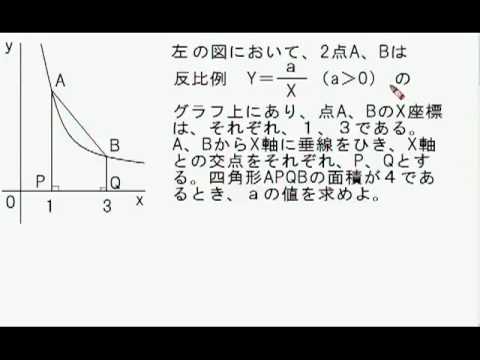



ご質問への解説 反比例グラフ応用 Youtube




比例反比例の応用 のグラフのx 0の部分に点cを取り Ocqの面積が Oa 中学校 教えて Goo




中1数学 反比例のグラフにみられる3つの特徴 Qikeru 学びを楽しくわかりやすく



中学生の数学講座 比例 反比例の利用 グラフ



無料 中1数学 発展問題 問題プリント 比例と反比例5 反比例のグラフ




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく




比例と反比例 6 反比例のグラフ 伊東市の家庭教師




比例と反比例 4 座標と比例のグラフ 伊東市の家庭教師



Mathematics 比例と反比例 式と座標 働きアリ




比例 反比例 きっずゼミ子育て応援ブログ




毎日問題を解こう 2 苦手な数学を簡単に



比例と反比例 中学数学の座標の読み方とグラフの式の求め方 Hatsudy 総合学習サイト
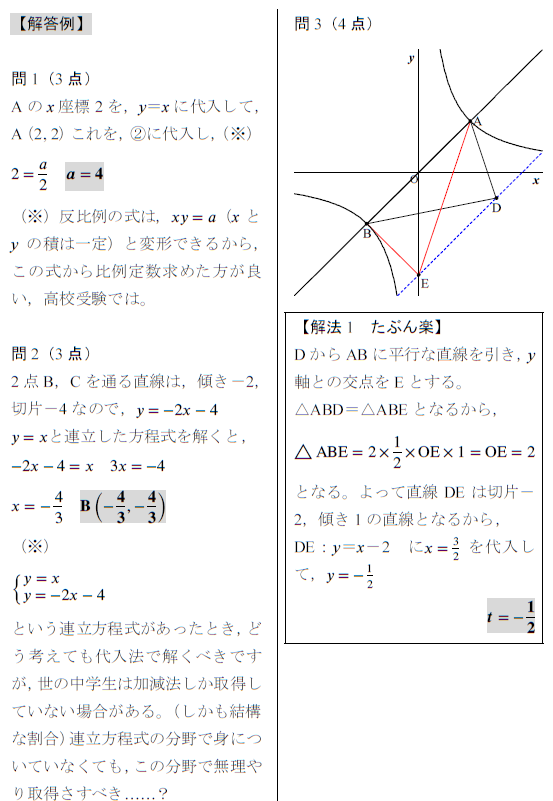



反比例と直線 オリジナル問題 高校入試 数学 良問 難問




中学数学1年 比例と反比例 Wikibooks



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典
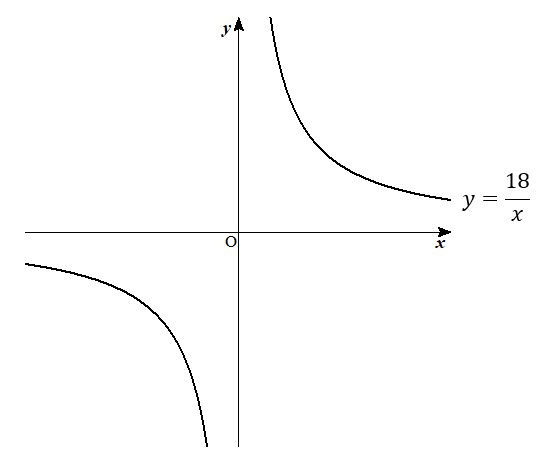



反比例 変域問題の解き方は グラフを使って丁寧に解説するぞ 数スタ
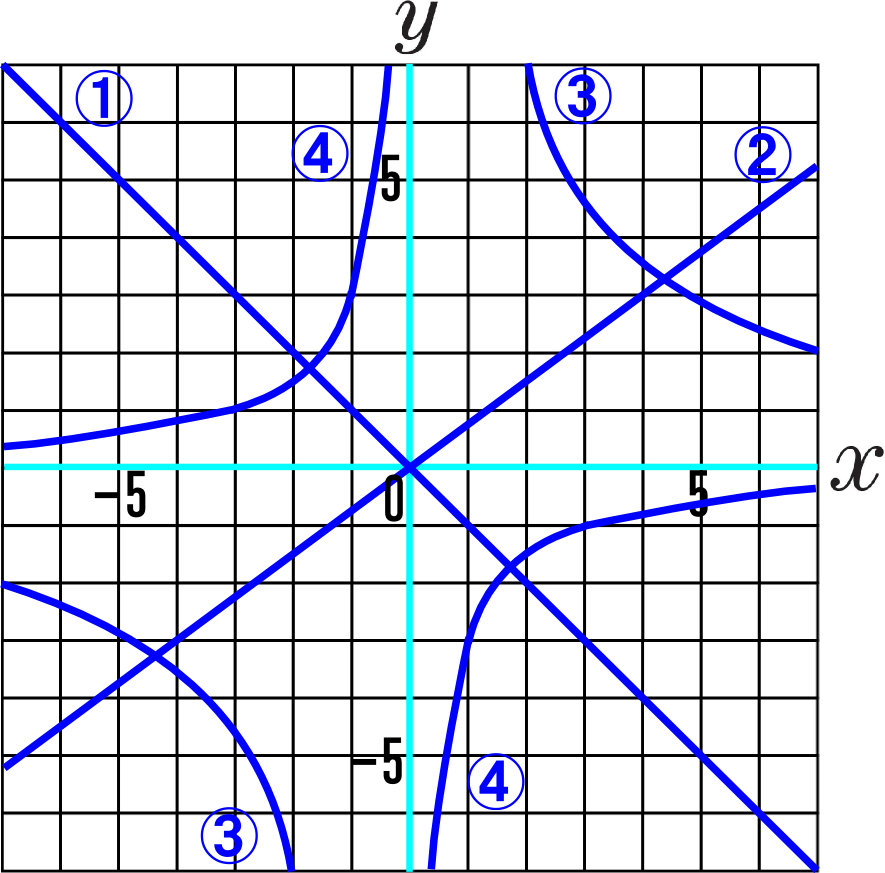



中学1年数学練習問題 比例 反比例のグラフ 関数 座標の復習テスト



1
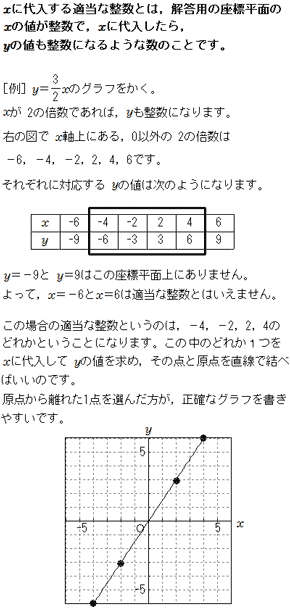



グラフをかくときの適当な整数とは 比例と反比例 中学生からの勉強質問 数学 進研ゼミ中学講座
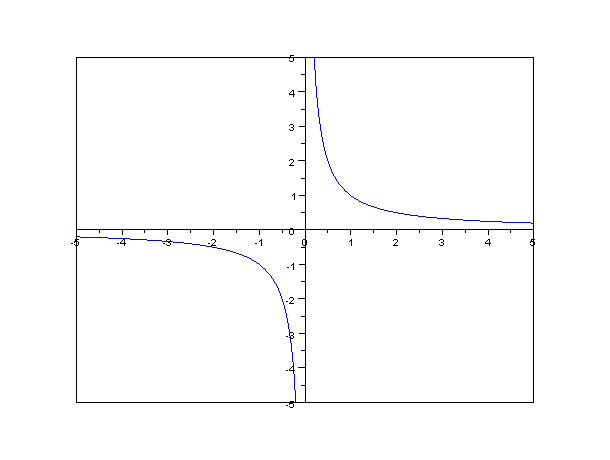



反比例 Wikipedia




基本 反比例のグラフ なかけんの数学ノート




中1 数学 中1 53 反比例のグラフを書く 読みとる Youtube
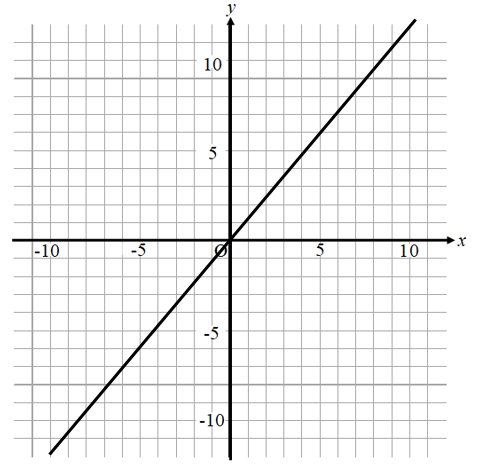



比例のグラフから式を求める方法とは ラクな裏技の考え方とは 数スタ
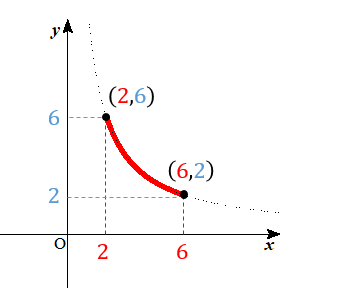



反比例 変域問題の解き方は グラフを使って丁寧に解説するぞ 数スタ
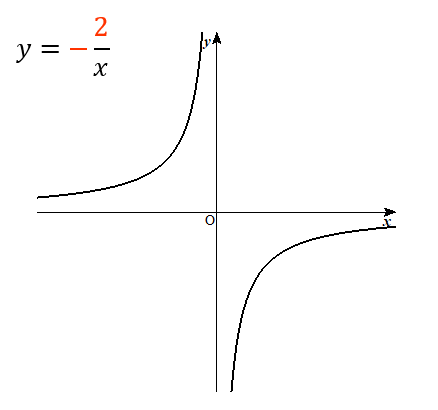



反比例のグラフの書き方 基礎からていねいにやってみよう 数スタ
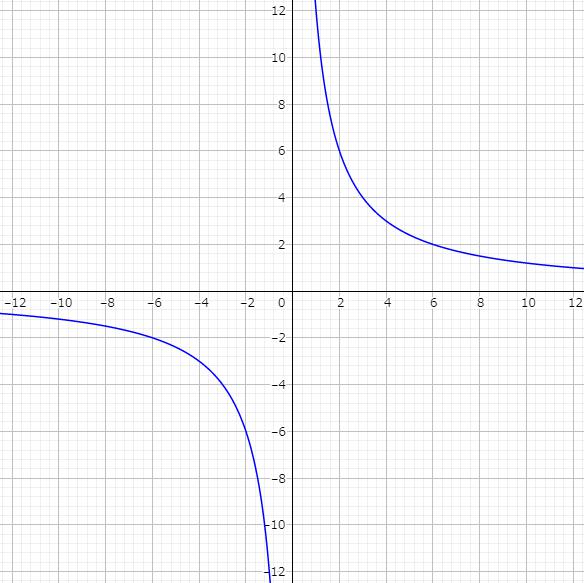



中1数学 反比例のグラフの書き方 Pikuu



中学1年数学練習問題 比例 反比例 反比例の関数とグラフの問題



3
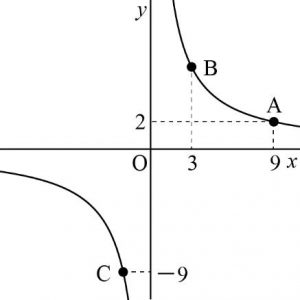



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院




一次関数とは 式とグラフの解説 数学fun




反比例とは何かが例で即わかる 公式 グラフの書き方も即理解 高校生向け受験応援メディア 受験のミカタ



Studydoctor比例 反比例のグラフと図形 中学1年数学 Studydoctor



1
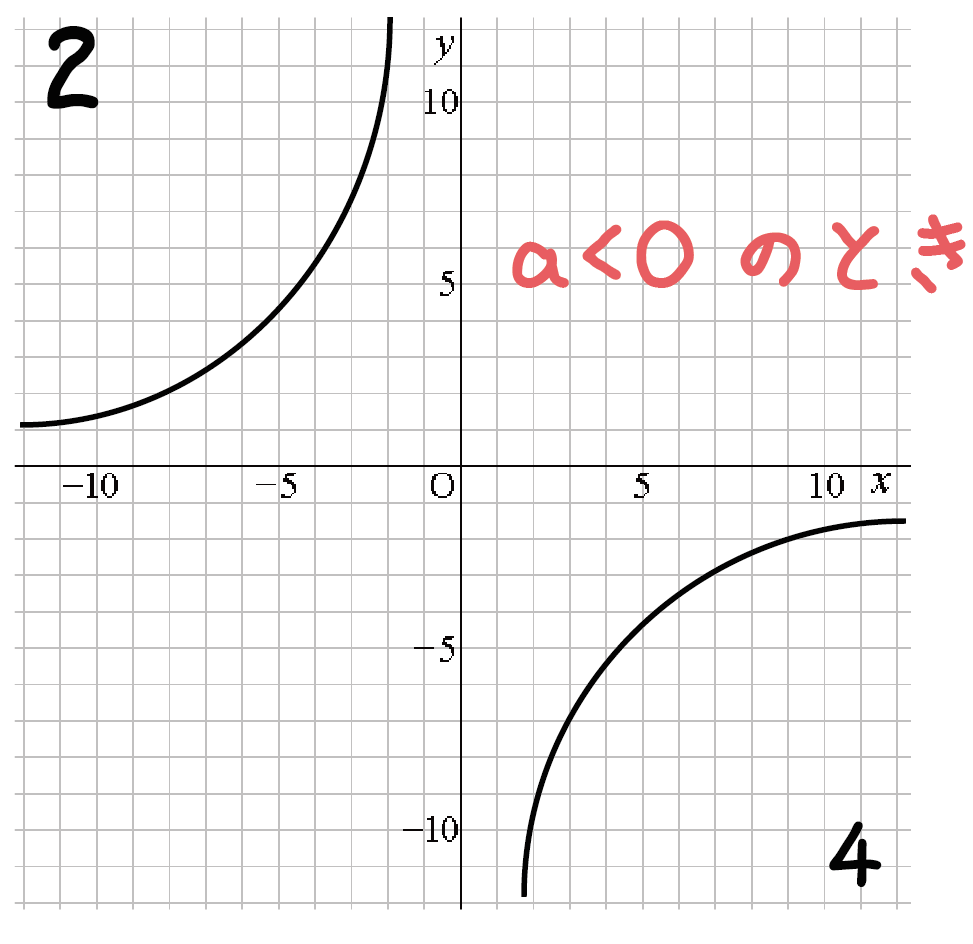



中1数学 反比例のグラフにみられる3つの特徴 Qikeru 学びを楽しくわかりやすく



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典
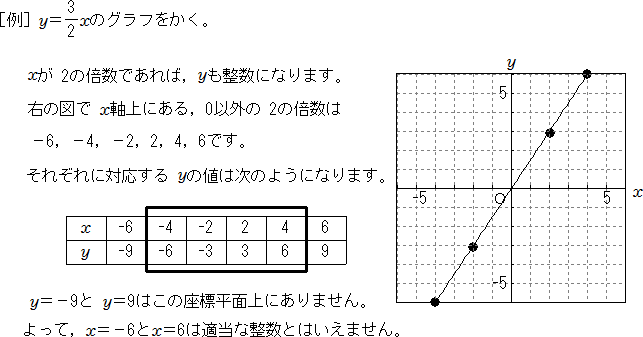



比例と反比例 グラフをかくときの適当な整数とは 中学数学 定期テスト対策サイト




中1数学 比例と反比例の活用 学習プリント 練習問題 無料ダウンロード印刷




中学数学1年 比例と反比例 Wikibooks




比例 反比例 一次関数 二次関数 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



0 件のコメント:
コメントを投稿