But avoid Asking for help, clarification, or responding to other answers The chain rule implies dx/dt = (dy/dt)/(dy/dx)" 1" Use implicit differentiation to obtain dy/dx Evaluate dy/dx at (2,3) Substitute the result and dy/dt into equation 1 Given 3x^2y2x=32 Verify that the point (2,3) lies on the curve 3(2)^2(3)2(2)=32 Use implicit differentiation 6xy3x^2dy/dx 2 = 0 3x^2dy/dx = 26xy dy/dx = (26xy)/(3x^2) Evaluate dy/dx at (2,3) dy/dx = (26(21 Verify that (4, 12) is the solution to the system Show work to justify your answer 2xy=5 5x2y=6 2 Solve the system by graphing State the solution x y =2 2y – x = 10 3 Solve the system by substitution State whether the system has one algebra
2
32(x+y)2-2x-2y
32(x+y)2-2x-2y-Y = g0(y) = 2y −2 = N In that case, g(y) = y2 −2y, and f(x,y) = x2 3xy2 −2y The implicit solution is x2 3xy2 −2y = C 2 Problem 3 (3x2 −2xy 2)dx(6y2 −x2 3)dy = 0 Check to see if the equation is exact M y = −2x N x = −2x So yes Now we'll antidifferentiate M with respect to x f(x,y) = Z M dx = Z 3x2 −2xy 2dx The equation is To change the expressions (x 2 2x) and (y 2 4y) into a perfect square trinomial,add (half the x coefficient)² and add (half the y coefficient)²to each side of the equation Compare the standardform of ellipse a 2 > b 2 If the larger denominator is under the "y " term, then the ellipse is verticalCenter (h, k )a = length of semimajor axis, b = length of semi
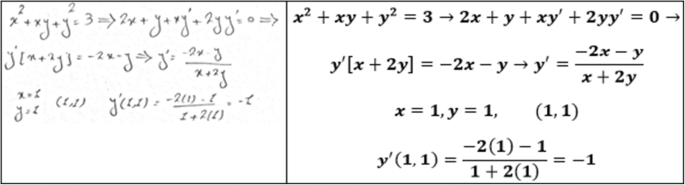



On Students Understanding Of Implicit Differentiation Based On Apos Theory Springerlink
– 4x 6y = 32 Find the equations of the lines which are tangent to tY (((((x 2)xy)2x)(2•——))2xy)y 2 x 2 Step 2 Rewriting the whole as an Equivalent Fraction 21 Subtracting a fraction from a whole Rewrite the whole as a fraction using x 2 as the denominator Thanks for contributing an answer to Mathematics Stack Exchange!
Solve the following equations by inversion method x 2y = 2, 2x 3y = 3 Maharashtra State Board HSC Science (General) 12th Board Exam Question Papers 231 Textbook Solutions Online Tests 73 Important Solutions 3704 Question Bank Solutions Concept Notes &Algebra questions and answers 1 1 1 Tit 1 1 7 (4x Y 2z = 11 3 X 2y 2 = 1 (2x 2y 32 = 1 8Algebra Calculator get free stepbystep solutions for your algebra math problems
Suppose x and y are rational solutions of x2 y2 = 3k, with k an odd integer Then k = 2j 1 (x2y)2 (xy)2 Final result 3y • (2x y) Step by step solution Step 1 11 Evaluate (x2y)2 = x24xy4y2 12 Evaluate (xy)2 = x22xyy2 Step 2 Pulling out like Click here 👆 to get an answer to your question ️ 32(xy)22x2y factorise bebydevi58 bebydevi58 3 weeks ago Math Secondary School answered 32(xy)22x2y factorise 1 See answer bebydevi58 is waiting for your help Add your answer and earn pointsStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 10x2y=32,2x2y=16 Tiger Algebra Solver




Answered X Y 22 U 0 2x 2y 32 2u O Bartleby



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q6 Pdf
Question 6 2x y z = a x 2y z = x y 32 = 7 x 2y 3z = a 2x 6y 112 = b 2x 4y 14z = 2c 8 If A = 1 = 3) and A = PQ, where P is a symmetric matrix and Q is aSolution for 2y=32 equation Simplifying 2y = 32 Solving 2y = 32 Solving for variable 'y' Move all terms containing y to the left, all other terms to the right Divide each side by '2' y = 16 Simplifying y−x y = 2 x 2y = 16 A Divide the second equation, 2x 4y = 32, by 2B Divide the first equation, −x eeduanswerscom



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline



2
Solution for 2x2y=32 equation Simplifying 2x 2y = 32 Solving 2x 2y = 32 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add '2y' to each side of the equation 2x 2y 2y = 32 2y Combine like terms 2y 2y = 0 2x 0 = 32 2y 2x = 32 2y Divide each side by '2' x = 16 1y Solve $$ (y^2 2x^2y)dx (2x^3 xy)dy = 0 $$ I tried to solve the differential equation in the following manner, but I am unable to arrive atदिया गया है 32 × (4x 2) = 2y प्रयुक्त सूत्र am × an = a(m n) यदि am = an तब m = n गणना 25




Solve Each System By The Method Of Your Choice Chegg Com




Ex 3 2 4 I Which Of The Pairs Of Linear Equations Are Consistent
X \displaystyle x x in the first equation, 1 We can add the two equations to eliminate x \displaystyle x x without needing to multiply by a constant x2y=−1 −xy=3 3y=2 x 2 y = − 1 − x y = 3 3 y = 2 Now that we have eliminated x \displaystyle x x, we What is the center and radius of 2x^22y^2=32?Question From NCERT Maths Class 9 Chapter 2 EXERCISE 24 Question – 5 POLYNOMIALS CBSE, RBSE, UP, MP, BIHAR BOARDQUESTION TEXTFactorise (i) `x^32x^2x




Linearalgebra03 Problem 2 Previous Problem List Next Previous Problem List Next 1 Point Find A Set Homeworklib




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
Solution for x z = 3 2y 2z = 2 2x z = 3 1 The matrix of the system A = 2 The value of matrix determinant JA 3 The adjoint matrix (adj A) = A circle has equation r?Y x = λ2x λ2y = 8x 2y so y2 = 4x2 or y = ±2x Sub into (6) to find 4x2 4x2 = 8 ⇒ x = ±1 Combiningwithy = ±2x, we get thesolutions (x,y) = (1,2),(1,−2),(−1,2) and (−1,−2) Since our constraint is closed and bounded, we can simply compare the value of f at these four points to determine the maximum and minimum values of f subjectGet answer Using matrices, solve the following system of equations xyz=2,2xy=3,2yz=0



Http Www Prosper Isd Net Cms Lib5 Tx Centricity Domain 52 4 3 elimination practice Pdf




Factorise The Following 32 X Y 2 2x 2y Brainly In
Graph y^2=32x y2 = 32x y 2 = 32 x Rewrite the equation as 32x = y2 32 x = y 2 32x = y2 32 x = y 2 Divide each term by 32 32 and simplify Tap for more steps Divide each term in 32 x = y 2 32 x = y 2 by 32 32 32 x 32 = y 2 32 32 x 32 = y 2 32 Cancel the common factor of 32 32Click here👆to get an answer to your question ️ If x^3 2x^2y^2 5x y 5 = 0 and y (1) = 1 then 25 X32 Y=2y2x=3 metodo de eliminación 1 Ver respuesta jhon32jdaniel está esperando tu ayuda Añade tu respuesta y gana puntos villalduvanfelipe villalduvanfelipe RespuestaEn los ejercicios 1 a 8 resuelva el sistema por el método de sustitución 1 x y 2 2 2x 3y 3 y 0 305x y 075 125x 45y 25 4 2x y 10 8x 3y 3 x 5y 6 2x 5y 28




If X Y 12 And X Y 32 Find The Value Of X2 Y2 Maths Polynomials Meritnation Com



Solved Find The Slope Of The Surface Z 2x Y X 2y At The Point 4 2 3 4 In Both The X Direction And The Y For F X Y Sin 2x 3 Course Hero
Click here👆to get an answer to your question ️ If 2^2x y = 32 and 2^x y = 16 then x^2 y^2 is equal toGuest 0 users composing answersGraph 2x^22y^2=32 Divide both sides of the equation by The variable represents the radius of the circle, represents the xoffset from the origin, and represents the yoffset from origin The center of the circle is found at Center These values represent the important values for graphing and analyzing a circle



Solve The System Of Linear Equations By Matrix Method X Y Z 3 2x Y Z 2 X 2y 3z 2 Mathematics Topperlearning Com Dqx3252pp




Answers
Systems of equations 1) {2x2y= 14 {x4y= 13 2) {yx= 17 {2y÷3x= 11 3) {x6y=1 {2x3y=32 Systems of equations 1) {2x2y= 14 {x4y= 13 2) {yx= 17 {2y÷3x= 11 3) {x6y=1 {2x3y=32 {x4y= 13 2) {yx= 17 {2y÷3x= 11 3) {x6y=1 {2x3y=32 Categories Uncategorized Leave a Reply Cancel reply Your email address will not be 👍 Correct answer to the question −x y = 2 2x 4y = 32 What action was completed to create this new equivalent system of equations? If the system of linear equations 2x 2y 3z =a 3x y 5z =b x 3y 2z =c where a, b, c are nonzero real numbers, has more than one solution, then 92k 1846k 218 966k
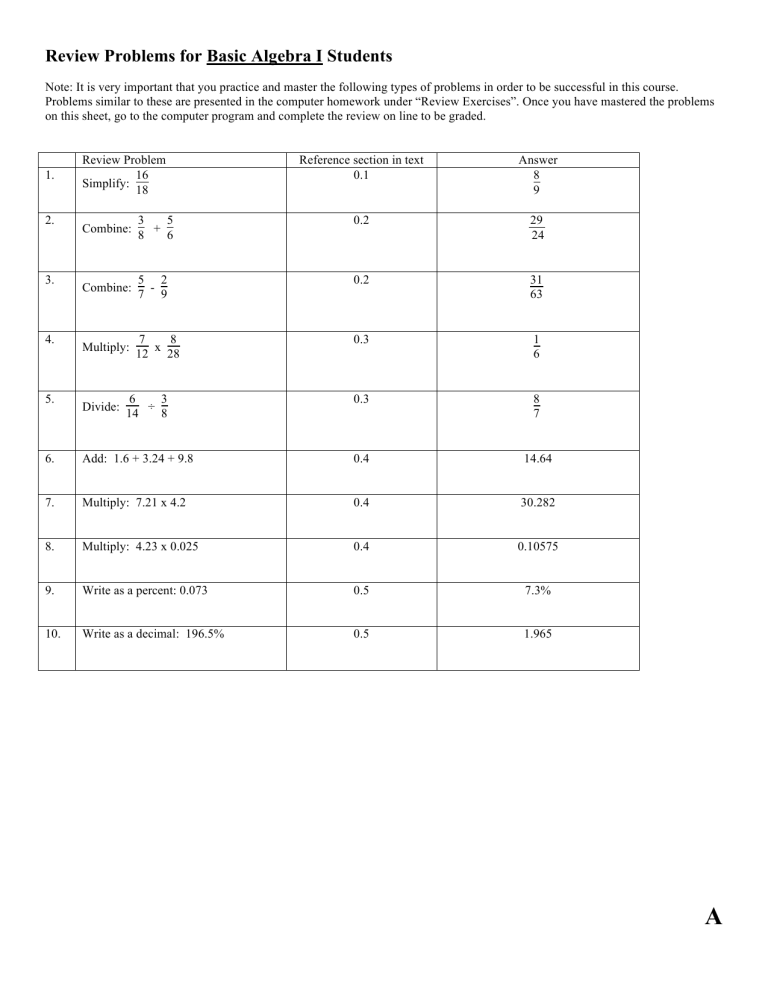



Review Problems For Basic Algebra I Students



2
x x 2y (y) = 17 2 or 3y = 15 Divide both sides by 3 y = 5 Put this back into the first equation x 2*5 = 17 x 10 = 17 x = 17 10 x = 7 B 4x 5y = 11 2x 6y = 16 Double all the terms in the second equation to get the number of x's the same as in the first equation 4x 12y = 32 Subtract the first equation from theFree system of equations calculator solve system of equations stepbystep Now that we have the y term, we can plug it into either equation to find x #2x6(4) = 32# #2x24=32# (Multiplied 6*4) #2x= 8# (Subtracted 24 from both sides) #x=4# (Divided both sides by 2) Check your answer y plugging in y=4 and x=4 into either equation




Solve 3 2x Y 8 X 2y 3 12 X 2y 6 2x Y 1 Brainly In
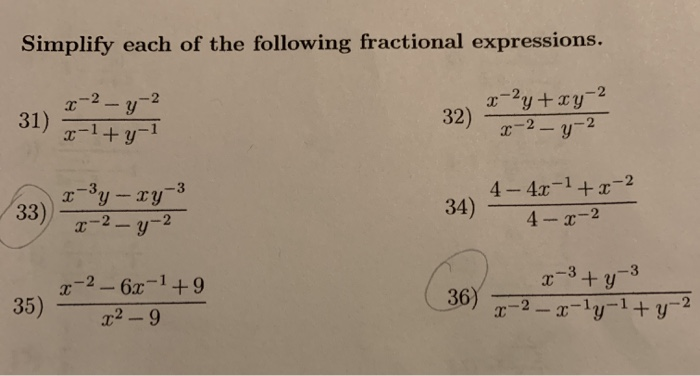



Simplify Each Of The Following Fractional Chegg Com
6(x2)=4(32x)=1 check to see that you copied the problem accuratelyyou have two equal signs 242(x1)15x=(3x17)5x 2x215x=3x175x 17x2=2x17 15x2=17 15x=15 x=1 2y3(42y)=6(y1)2 8y126y=6y62 14y12=6y4 8y12=4 8y=16 y=2 324(2x5)3x=x28 8x3x=x285x=x286x=286x=48 x=8 364(2x5)3x=xx28 8x3x=2xResultado de 3y2y=32 3y2y=32 Movemos todos los personajes a la izquierda 3y2y(32)=0 Sumamos todos los números y todas las variables y32=0 Movemos todos los términos que contienen y al lado izquierdo, todos los demás términos al lado derecho y=32 El resultado de la ecuación 3y2y=32 para usar en su tarea domésticaयदि 2x 3y 5z = 18, 3x 2y z = 29 और x y 3z = 17 है, तो xy yz zx का मान क्या है?



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q6 Pdf



2
Please be sure to answer the questionProvide details and share your research! Solve the system of equations by graphing Then classify the system xy=9 xy=3 Use graphing tool to graph the system Algebra Find the number of the solutions to each system a 4xy1=0 4xy3=0 b 2xy4=0 4x2y8=0 Write a question that can be solved using a system of linear equationsLet us break the expression and write the terms separately (2x^2–4x)(3y^2–12y)18 take the common values out 2×(x^2–2x)3×(y^2–4y)18 to make them perfect values we must add & subtract the constantsThe following expression can be written as {2×
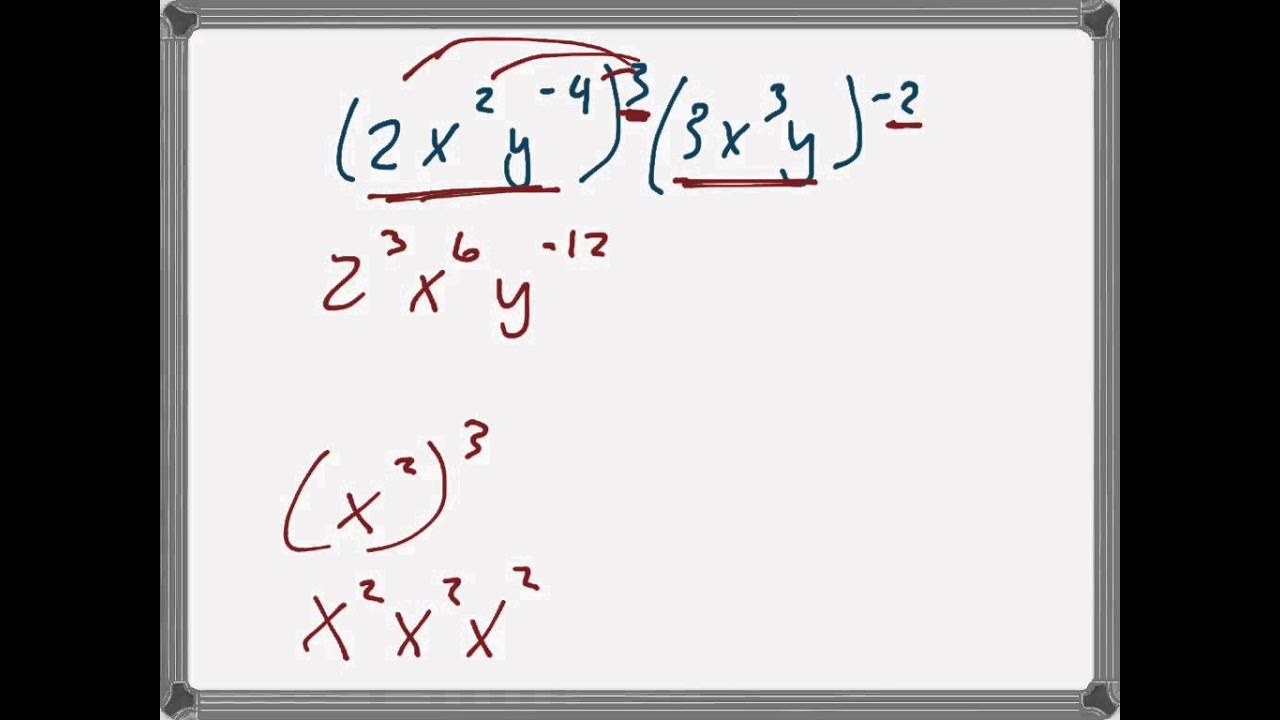



Simplify 2x 2y 4 3 3x 3y 2 Youtube



Http Lphs Alpineschools Org Wp Content Uploads Sites 5 Herring Secondary math 2 Worksheets Term 4 Systems 2 2 Pdf
3x 7y=78 consider it as equation 1 x3y=32 consider it as equation 2 for finding the value of 2 variables (here x and y) ,we need 2 equations by solving then with elimination process first we have to make coefficients of either x or y equal soThese are the numbers on the right of the equal signs in the system, ie, the red numbers below 2x3y3z=25 3x1y1z=5 5x2y4z=32 Here is D x 253 3 5 1 1 322 4 y is the SECOND unknown that appears, so D y is just like D except that the SECOND column is replaced by the column of constantsExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music



Simultaneous Equations Forming Solving Card Match Ppt Download




Systems Of Equations With Substitution Y 1 4x 100 Y 1 4x 1 Video Khan Academy
2 Estudia y resuelve por el método de Gauss –x y 3z = –2 y z = –1 a) *4x 2y – z = 5 b) *x – y = 1 2x 4y – 7z = 1 x 2y 3z = –2 5x 2y 3z = 4 x – y 3z – 14tRelated Questions यदि 2x 3y 5z = 18, 3x 2y z = 29 और x y 3z = 17 है, तो xy PQR is an equilateral triangle whose side is 10 cmVariable x cannot be equal to any of the values 8,4 since division by zero is not defined Multiply both sides of the equation by \left(x4\right)\left(x8\right)




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf



2
If 2x^2 λxy 2y^2 (λ – 4) x 6y – 5 = 0 is the equation of a circle, then its radius is A 3√2 B 2√3 C 2√2 D none of the above ← Prev Question Next Question → 0 votesAdd both of them, and equate it to 1 and solve in sinx or cosx in any of them by writing cosx = 1 – sin^2x or vice versa get x values and then simply y values and then u can find the final value Disapproved Abhinav Anand 10 PointsTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW 2x 3 y 3z =5 , x 2y z=4 , 3x y2z = 3




Factorise The Following 32 X Y Sq 2x 2y Mathematics Topperlearning Com W0twcmff



Solved Solve Each System Using Elimination 1 Xty 2 2 X 2y 3 3 2x Y 4 X Y 4 X Y 6 3x Y 2 4 X 2y 2 5 X 3y 3 6 X Course Hero
Factorise (i) x 3 2x 2 x 2 (ii) x 3 3x 2 9x 5 iii) x 3 13x 2 32x (iv) 2y 3 y 2 2y 1 Solution (i) Let p(x) = x 3 2x 2 x 2 By the factor theorem we know that x a is a factor of p (x) if p (a) = 0 We shall find a factor of p(x) by using some trial value of x, say x = 1 p(1) = (1) 3 2(1) 2 1 2 = 1 2 2) Parabola is the locus of points that are equidistant to the focus and the directrix If P(x,y) is a point on the parabola, then The square of its distance to the focus F(2,3) is




Factorise 32 X Y 2 2x 2y



2




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy




How Do You Find The Volume Of The Solid Generated By Revolving The Region Bounded By The Graphs Y 2x 2 Y 0 X 2 About The X Axis Y Axis The Line Y 8 The Line X 2



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf
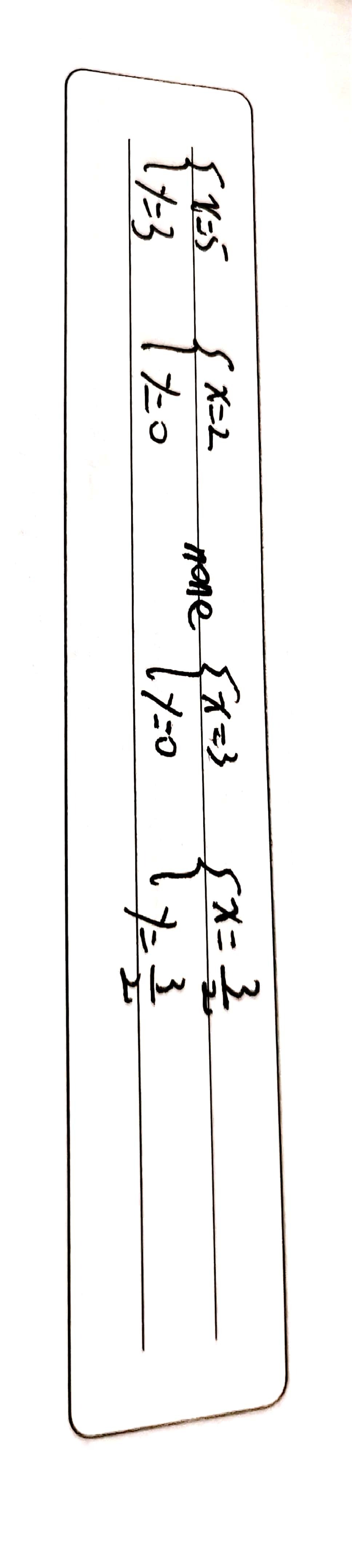



Ftbeginarrayl X Y 2 2x Y 13endarray Gauthmath




2 2x Y 3z 2 X Y 2 3 3x 2y 3z 1 Gauthmath




Answered 2 V Cycz 2 Cxy 2cx2 3 V Bartleby



2
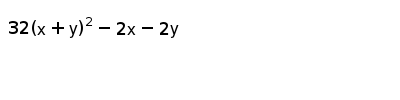



Example 3 Find The Inverse Of The Matrix1 2 3ai 2 31 2 3and Henc
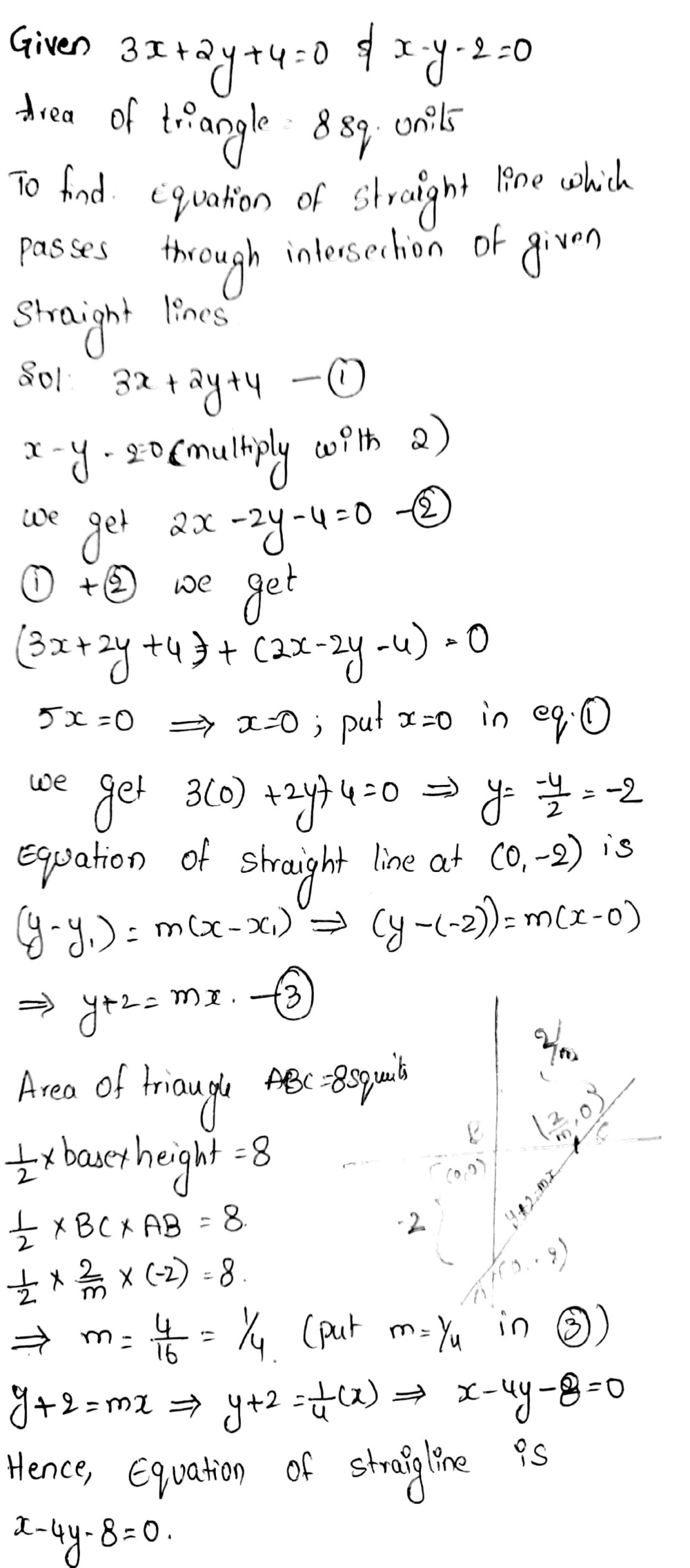



Find The Equation Of Straight Line Which Passes Through The Intersection Of The Straight Lines 3x 2y 4 0 And X Y 2 0 And Forms A Triangle With The Axes Of Area 8 Sq Units Snapsolve




Ns 2 6 Solve Each Sys Of E R X 2y 2 4 2x Y 32 8 2x Chegg Com




3x 2y 3 2x Y 16 Find The Values Of Determinants In The Given Equations D Dx Lisil 38 D 2 L Le Values According To Cramer S Rule 35 42 X X Y 5 7 6 Is The Solution 15



Http Petalschools Com Cms Lib03 Ms Centricity Domain 455 hw 12 3 Pdf




Solve The Following System Of Linear Equations By Matrix Method X Y Z 3 2x Y Z 2 X 2y 3z 2 Youtube




Mathalino Goals Cttro Of Pic 2 X Y 32 2 X Y 2 5 X Y 5 3 3x 2y 243 3 3x 2y 3 5 3x 2y 5 X Y 5 Y 5 X 3x 2 5 X 5 3x 10 2x 5 5x 10 5 5x 5 10 5x 15 X 3 Y 5 X Y 5 3 Y 2 Facebook




Solutions To Implicit Differentiation Problems




Engineering Mathematics Notes




X 2y 3 2 2x Y 3 2 Solve This Equation Using Substitution Method Brainly In
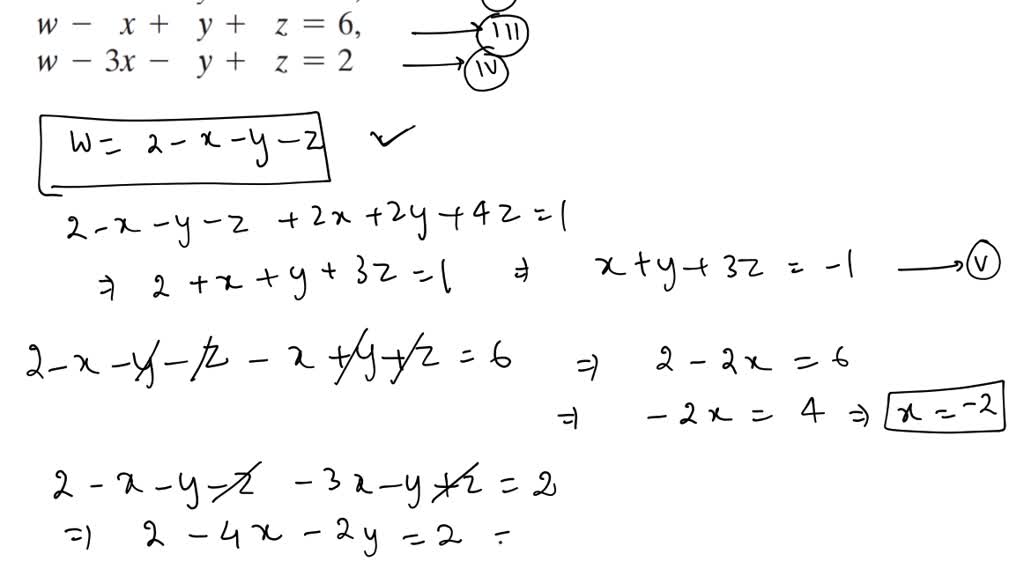



Solved Solve Begin Array L W X Y Z 2 W




Solve Division Of Polynomials Step By Step Math Problem Solver
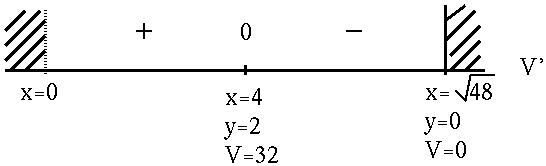



Solutions To Maximum Minimum Problems



Solve Dy Dx X 2y 3 2x 3y 4 Sarthaks Econnect Largest Online Education Community




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6



Http Math Utoledo Edu Dwhite1 D 2850 T2a2850soln Pdf
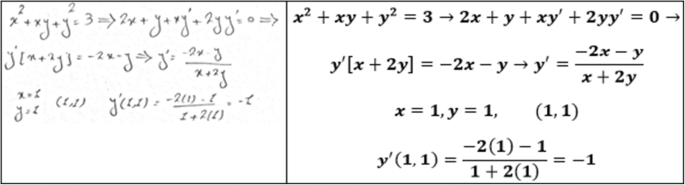



On Students Understanding Of Implicit Differentiation Based On Apos Theory Springerlink




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community



2



Www Umtsd Org Cms Lib Pa Centricity Domain 461 Sm Entering Geometry Pdf




Answered 0 Is Cnte Raph Costai Function 229en Bartleby




Engineering Mathematics Notes



2




University Calculus Elements With Early Transcendentals 1st Edition H



2



If Math X Y 2 Text And X 2 Y 2 2 Math What Is The Value Of Math Xy Math Could You Break It Down For Me Quora



Www Thatonemathguy Com Uploads 7 0 1 3 Ch 3 Pdf




If 2x 2 2y 2 2x 2y 1 0 Then What Is The Value Of X Y Quora



2




Find The Minimum Value Of X 2 4xy 4y 2 2z 2 Given That Xyz 32 Mathematics Stack Exchange




Schaum S Outline College Algebra Pdf Txt
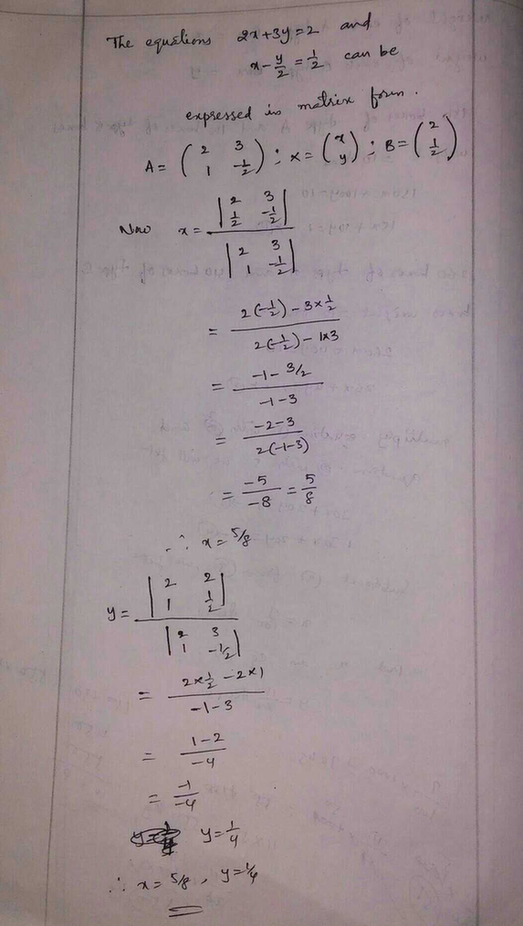



2x 3y 2 X Y 2 1 2 Using Cramer S Rule Scholr



2
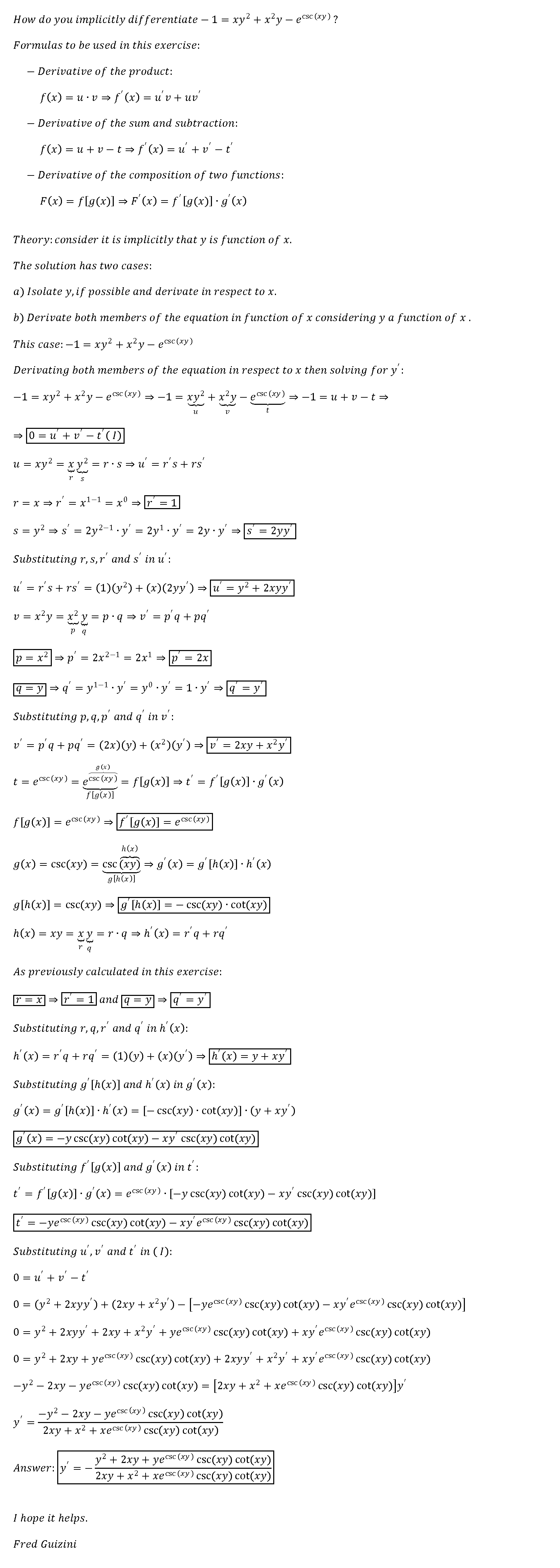



How Do You Implicitly Differentiate 1 Xy 2 X 2y E Csc Xy Socratic




Solve Division Of Polynomials Step By Step Math Problem Solver




If 2x Y 2 5 3x Y 1 3 2 X 2y 1 6 Then




The Perfect Square College Algebra Binomial Multiplication Foil When Multiplying Two Binomials Together We Can Use Foil Method F Product Of First Terms O Product Of Outer




Polynomials If X Y 12 And Xy 32 Find X 2 Y 2 Youtube




Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook



Www Colonialsd Org Uploaded Forms And Documents Curriculum Math Integrated Math Green Unit 3 Solving A System Of Linear Equations By Graphing Pdf




Solving Systems Of Equations By Graphing Bingo Card
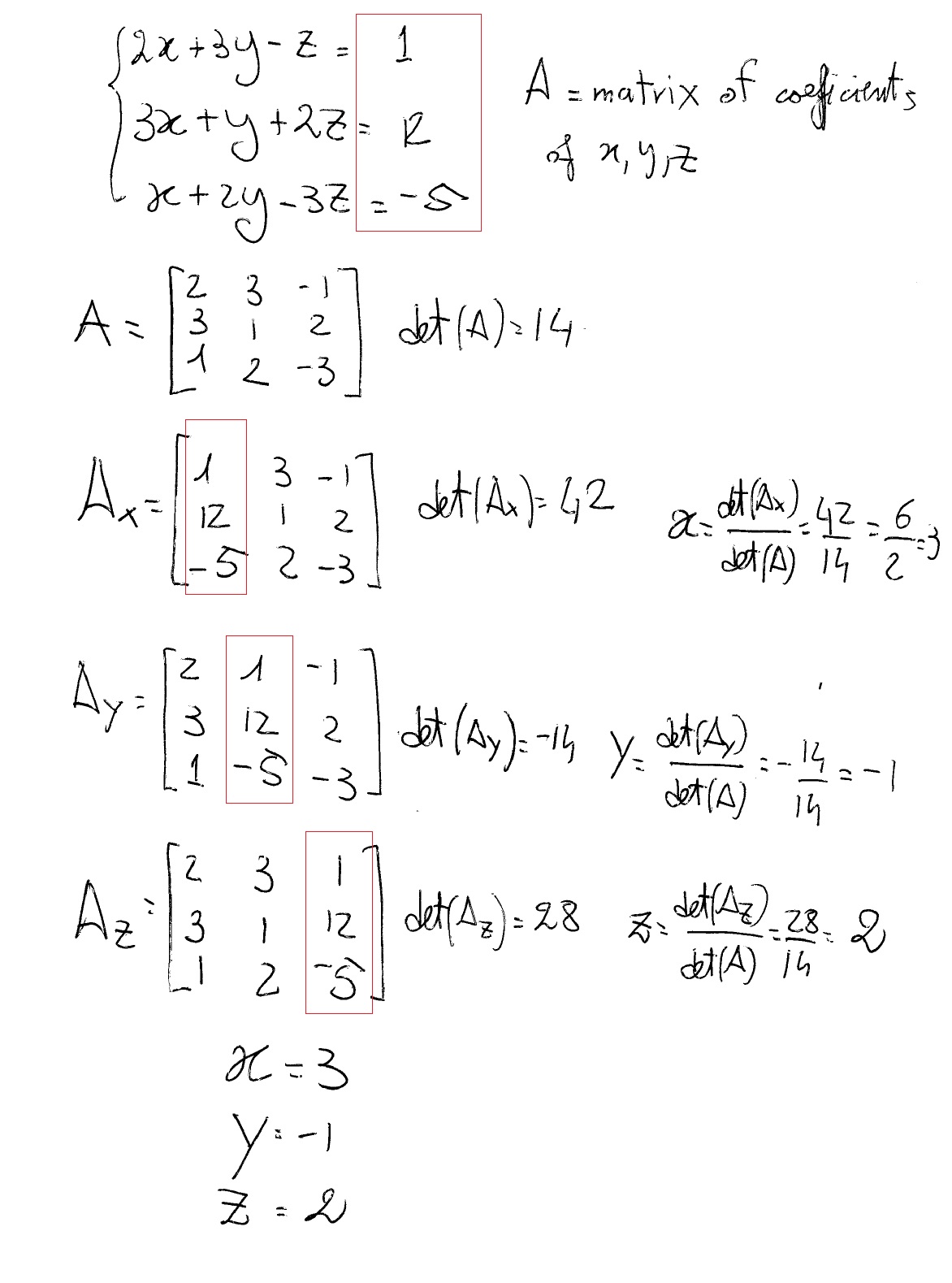



How Do You Solve 2x 3y Z 1 3x Y 2z 12 And X 2y 3z 5 Socratic




15 Three Lines X 2y 3 0 X 2y 70 And 2x Y 4 0 Form The T Scholr



2




Math 4 Chapter 7 1 Solving Systems Of Linear Equations Oneclass



2



2




32 X Y 2 2x 2y Youtube




If A 2 3 1 1 2 2 3 1 1 Find A 1 And Hence Solve The System Of Equations 2x Y 3z 13 3x 2y Z 4 X 2y Z 8 Mathematics Shaalaa Com




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf




3 2 Implicit Equations And Implicit Differentiation




Please Only Solve 36 With The Steps The Last Line Is Chegg Com




Personal Lnde Page 32 33 Created With Publitas Com



2



Www Utdallas Edu Efrom Solhw Pdf




100 Advanced Mathematics Ideas In 21 Advanced Mathematics Mathematics Advanced Physics




6 32 X Y 2x 2yfactorise It Brainly In



How To Factorise 3 X Y 2 2 X Y Quora




For X Y In Nn If 3 2x Y 1 3 Y 2x 1 8 And Log 6 2x 2y X Y 2 1 Log 36 X Y Then Find The Absolute Value Of X Y




26 If F X 2y X 2y Xy Then F X Y Is Equal




Find The General Solution Of Xy 3 2x Y 2y 2 Chegg Com




3 2x Y 2 2x Y 1 2x 5y Frac Y24x2 Y2 Gauthmath



0 件のコメント:
コメントを投稿